randformblog on math, physics, art, and design |
You have probably seen this video where the duchess Kate Middleton rolls her eyes after being told “keep wrapping” during a charity visit within the US. Since it is the holiday season randform now proudly presents the exclusive footage on WHAT the duchess was actually told to wrap.
We here at randform are superexcited to present our first reader randform mega contest – simply called LeContest !!
Unfortunately our temperature visualization from last post is currently not running anymore. Probable reason: It currently seems that WebGl Earth has moved two library files. In particular the WebGl earth API base script which we were thinking was self-contained unfortunately doesn’t seem to be self-contained. We are going to look at this trouble in the near future.
supplement 05.10.2014: The interactive visualization is currently working again. Klokan technologies had responded and promised to look into this problem.
As was announced in the last post Tim and me were working at a visualization of the data collection CRUTEM 4 by the climate research unit (CRU) at the University of East Anglia. In the post it was mentioned that the data in that collection was sort of “deteriorating”. That is on one hand the number of active temperature measurement stations which were listed in this file (some stations started measuring already in the 18th century) decreased rather rapidly in the last ten years and/or the file contained increasingly invalid/no temperature data in the last ten years.
In that context it is worthwhile to note that CRUTEM 4 supercedes CRUTEM 3 and the CRUTEM 3 (grid data) was according to the Intergovernmental panel on Climate Change (IPCC) used for the IPCC fourth assessment report (AR 4).
Wether the “deterioration of that CRUTEM 4 data” has any effect on the assessment of the current global warming trends is another question. The application is now online. Explore yourself! Caution the data takes very long to load. The CRUTEM 4 data file is about 45 MB.
The following two interactive applications also display global temperature data:
– HADCRUT 3 (which uses CRUTEM 3) data is visualized here by Cliff Best.
– NOAAs Global Historical Climatology Network-Monthly (GHCN-M) is visualized here by Nick Stoves.
– our comparision of temperature anomalies, CO2 and methane values uses HADCRUT 4 which uses CRUTEM 4 and HadSST3 (sea surface temperatures).
warning: 18.10.2014
Unfortunately the application is currently not running anymore. Probable reason: It currently seems that WebGl Earth has moved two library files. In particular the WebGl earth API base script which we were thinking was self-contained unfortunately doesn’t seem to be self-contained. We are going to look at this trouble in the near future.
supplement 05.10.2014: The interactive visualization is currently working again. Klokan technologies had responded and promised to look into this problem.
Tim and me are currently working on a interactive browser visualization using temperature data from HADCRUT, namely the CRUTEM 4 temperature station data which we map with the help of the open source web GL earth API (which seems to be to quite some extend the work of the Czech-Swiss company Klokan technologies) onto a model of the earth (covered with open street maps).
The visualization is still work in progress, but what is already visible is that the temperature data is quite deteriorating (please see also the previous randform post on the topic of deteriorization of data). Where it looks as if the deterioration had been bigger in the years from 2000-2009 than in the years 1980-2000. Below you can see screenshots of various regions of the world for the month of January for the years 1980, 2000 and 2009. The color of a rectangle indicates the (monthly) temperature value for the respective station (the station is represented by a rectangle around its coordinates) which is encoded with the usual hue encoding (blue is cold, red is hot). Black rectangles are invalid data. The CRUTEM 4 data file contains the data of 4634 stations. Mapping all the station data makes the visualization very slow, especially for scaling, therefore the slightly different scalings/views for each region and the fact that screenshots are on display. The interactive application will probably be not for all stations at once.
North America:
Jan 1980
Jan 2000
Jan 2009
Africa:
Jan 1980
Jan 2000
Jan 2009
Asia:
Jan 1980
Jan 2000
Jan 2009
Eurasia/Northern Africa:
Jan 1980
Jan 2000
Jan 2009
Northpole:
Jan 1980
Jan 2000
Jan 2009
update June 15, 2019:
There is now a similar interactive visualization at NASA for the GHCN data set at https://data.giss.nasa.gov/gistemp/stdata/
update December 29, 2021:
The link to our interactive temperature visualization, which was announced above in the post is here, the corresponding post about it is here.
The GHCN page linked on June 15, 2019 doesn’t show any station data anymore:
There is currently a new page with a “version 4 dataset” here. This is how it currently looks like:
Apriori this looks as if most of the stations are “back on track” but then I couldn’t find out within a decent time how much of this data is “reconstructed” in the sense of “educated guess” and how much is actual data from the respective stations. Another thing that caught my attention was that the content of the tooltipmenu of each station is partially non accessible, I don’t remember whether this is a new phenomenon.
I am still collecting data on global employment in order to better investigate the replacement of human work by machines. Unfortunately it turned out that the International Labour Organisation (ILO), which holds most of the original data restructured their IT-sector. This means in particular that some older data can’t be reproduced any more. Above you can see that the worldwide employment went down on average since the nineties. I keep the data now here locally on our account as a copy from ILO in order to keep the findings reproducible. The data source as well as the source code for extracting it (GPL) are here. As always: if you spot some mistakes please let me know.
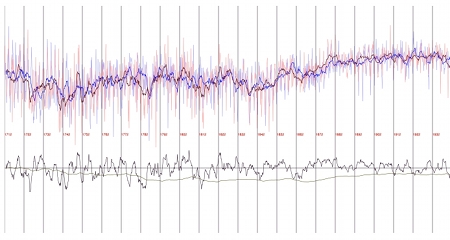
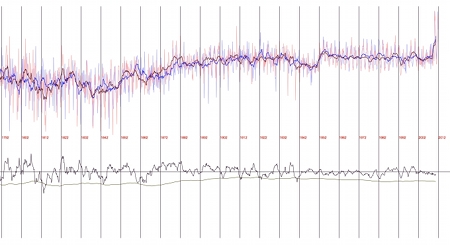
This concerns a discussion on Azimuth. I found that the temperature anomaly curve, which describes the global combined land [CRUTEM4] and marine [sea surface temperature (SST)] temperature anomalies (an anomaly is a deviation from a mean temperature) over time (HADCRUT4-GL) has a two-year periodicity (for more details click here). The dots in the above image shall display, why I think so. The dark line drawn over the jagged anomaly curve is the mean curve. The grey strips are one year in width. A dot highlights a peak (or at least an upward bump) in the mean curve. More precisely there are:
18 red dots which describe peaks within grey 2-year interval
5 yellow dots which describe peaks out of grey 2-year interval
(two yellow peaks are rather close together)
1 uncolored dot which describes no real peak, but just a bump
4 blue dots which describe small peaks within ditches
One sees that the red and yellow dots describe more or less all peaks in the curve (the blue dots care about the minor peaks, and there is just one bump, which is not a full peak). The fact that the majority of the red and yellow dots is red, means that there is a peak every 2 years, with a certain unpreciseness which is indicated by the width of the interval.
Upon writing this post I saw that I forgot one red dot. Can you spot where?
Especially after doing this visualization this periodicity appears to me meanwhile so visible that I think this should be a widely known phenomenom, however at Azimuth nobody has heard yet about it. If its not a bug then I could imagine that it could at least partially be due to differences in the solar irradiance for northern and southern hemissphere, but this is sofar just a wild guess and would need further investigations, which would cost me a lot of (unpaid) time and brain. So if you know how this phenomen is called then please drop a line. If its not a bug then this phenomen appears to me as an important fact which may amongst others enter the explanation for El Niño.
“In flagranti”, image from the art series “detective stories” by Massimo Mascarpone
This is just a a very brief follow-up to my last post in which I was looking at the market sizes of virtual assets.
techdirt has a blog post in which it is described that apparently the NSA uses gamification for making the use of the XKeyscore system more appealing.
I guess although here a game is used as an introduction for a virtual application this type of game wouldn’t fall into the free-to-play category, from superdataresearch:
One important trend in this context is the emergence of free-to-play or virtual goods revenue model. It allows the next generation of gamers to try a game before they commit any money, offering them a smooth introduction to games rather than asking for $50-$60 at the door.
